uniform gravitational field without air resistance[edit]
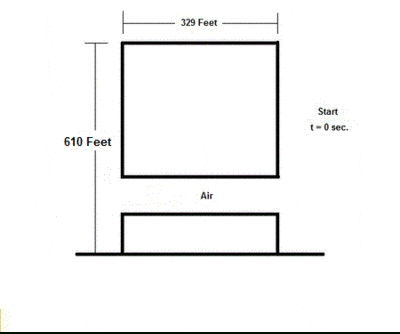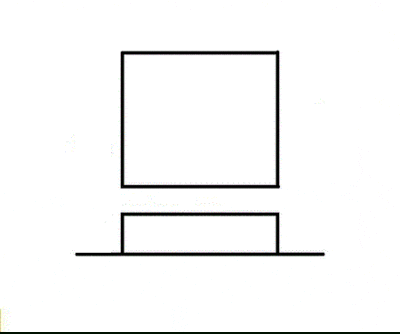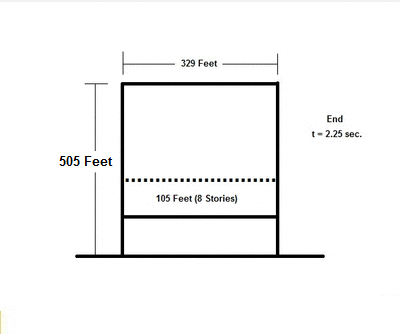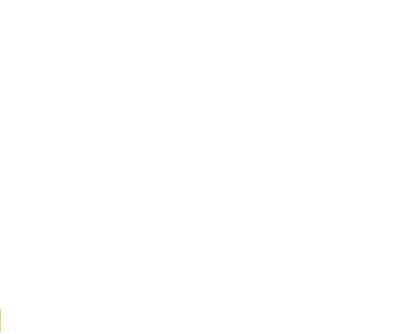
This is the "textbook" case of the vertical motion of an object falling a small distance close to the surface of a planet. It is a good approximation in air as long as the force of gravity on the object is much greater than the force of air resistance, or equivalently the object's velocity is always much less than the terminal velocity (see below).
Free-fall
v(t)=-gt+v_{0}\,
y(t)=-\frac{1}{2}gt^2+v_{0}t+y_0
where
v_{0}\, is the initial velocity (m/s).
v(t)\, is the vertical velocity with respect to time (m/s).
y_0\, is the initial altitude (m).
y(t)\, is the altitude with respect to time (m).
t\, is time elapsed (s).
g\, is the acceleration due to gravity (9.81 m/s2 near the surface of the earth).
Uniform gravitational field with air resistance[edit]
Acceleration of a small meteoroid when entering the Earth's atmosphere at different initial velocities.
This case, which applies to skydivers, parachutists or any body of mass, m, and cross-sectional area, A, with Reynolds number well above the critical Reynolds number, so that the air resistance is proportional to the square of the fall velocity, v, has an equation of motion
m\frac{dv}{dt}=\frac{1}{2} \rho C_{\mathrm{D}} A v^2 - mg \, ,
where \rho is the air density and C_{\mathrm{D}} is the drag coefficient, assumed to be constant although in general it will depend on the Reynolds number.
Assuming an object falling from rest and no change in air density with altitude, the solution is:
v(t) = -v_{\infty} \tanh\left(\frac{gt}{v_\infty}\right),
where the terminal speed is given by
v_{\infty}=\sqrt{\frac{2mg}{\rho C_D A}} \, .
The object's speed versus time can be integrated over time to find the vertical position as a function of time:
y = y_0 - \frac{v_{\infty}^2}{g} \ln \cosh\left(\frac{gt}{v_\infty}\right).
Using the figure of 450 metres to reach terminal speed, this equation implies a free-fall time to terminal velocity of around 12 seconds. However, when the air density cannot be assumed to be constant, such as for objects or skydivers falling from high altitude, the equation of motion becomes much more difficult to solve analytically and a numerical simulation of the motion is usually necessary. The figure shows the forces acting on meteoroids falling through the Earth's upper atmosphere. HALO jumps, including Joe Kittinger's and Felix Baumgartner's record jumps (see below), and the planned Le Grand Saut, also belong in this category.[2]
Inverse-square law gravitational field[edit]
It can be said that two objects in space orbiting each other in the absence of other forces are in free fall around each other, e.g. that the Moon or an artificial satellite "falls around" the Earth, or a planet "falls around" the Sun. Assuming spherical objects means that the equation of motion is governed by Newton's Law of Universal Gravitation, with solutions to the gravitational two-body problem being elliptic orbits obeying Kepler's laws of planetary motion. This connection between falling objects close to the Earth and orbiting objects is best illustrated by the thought experiment Newton's cannonball.
The motion of two objects moving radially towards each other with no angular momentum can be considered a special case of an elliptical orbit of eccentricity e = 1 (radial elliptic trajectory). This allows one to compute the free-fall time for two point objects on a radial path. The solution of this equation of motion yields time as a function of separation:
t(y)= \sqrt{ \frac{ {y_0}^3 }{2\mu} } \left(\sqrt{\frac{y}{y_0}\left(1-\frac{y}{y_0}\right)} + \arccos{\sqrt{\frac{y}{y_0}}}
\right)
where
t is the time after the start of the fall
y is the distance between the centers of the bodies
y0 is the initial value of y
μ = G(m1 + m2) is the standard gravitational parameter.
Substituting y=0 we get the free-fall time.
The separation as a function of time is given by the inverse of the equation. The inverse is represented exactly by the analytic power series:
y( t ) = \sum_{n=1}^{ \infty }
\left[
\lim_{ r \to 0 } \left(
{\frac{ x^{ n }}{ n! }}
\frac{\mathrm{d}^{\,n-1}}{\mathrm{ d } r ^{\,n-1}} \left[
r^n \left( \frac{ 7 }{ 2 } ( \arcsin( \sqrt{ r } ) - \sqrt{ r - r^2 } )
\right)^{ - \frac{2}{3} n }
\right] \right)
\right]
Evaluating this yields:
y(t)=y_0 \left( x - \frac{1}{5} x^2 - \frac{3}{175}x^3
- \frac{23}{7875}x^4 - \frac{1894}{3931875}x^5 - \frac{3293}{21896875}x^6 - \frac{2418092}{62077640625}x^7 - \cdots \right) \
where
x = \left[\frac{3}{2} \left( \frac{\pi}{2}- t \sqrt{ \frac{2\mu}{ {y_0}^3 } } \right) \right]^{2/3}
For details of these solutions see "From Moon-fall to solutions under inverse square laws" by Foong, S. K., in European Journal of Physics, v29, 987-1003 (2008) and "Radial motion of Two mutually attracting particles", by Mungan, C. E., in The Physics Teacher, v47, 502-507 (2009).
Free fall - Wikipedia, the free encyclopedia