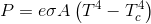So does heat radiates from cooler to warm?
Plug in the temperature of the cool object.
That tells you how much it radiates.
Now plug in the temperature of the warm object.
That tells you how much it radiates.
You see, they both radiate at the same time.
But the formula states, e.g. 200F- 100F = 100F, it's all one way. There's no heat flowing upstream.
But the formula states, e.g. 200F- 100F = 100F, it's all one way.
The formula does not state one way.
There's no heat flowing upstream.
Who said anything about heat? We're discussing radiation. Power emitted.
Heat Transfer Through Conduction: Equation & Examples - Video & Lesson Transcript | Study.com
Q over
t is the rate of heat transfer - the amount of heat transferred per second, measured in Joules per second, or Watts.
kis the thermal conductivity of the material - for example, copper has a thermal conductivity of 390, but wool has a thermal conductivity of just 0.04.
T1 is the temperature of one object, and
T2 is the temperature of the other. Since it's a temperature difference, you can actually use Celsius or Kelvin, whichever is most convenient. And
d is the thickness of the material we're interested in. So the rate of heat transfer to an object is equal to the thermal conductivity of the material the object is made from, multiplied by the surface area in contact, multiplied by the difference in temperature between the two objects, divided by the thickness of the material.
Calculation Example
Okay, let's go through an example. Let's say you're going to a water park, and you're going to take a Styrofoam cooler with you. The cooler has a total surface area of 1.2 meters squared, and the walls are 0.03 meters thick. The temperature inside the cooler is 0 Celsius, and at the hottest part of the day it's 38 degrees Celsius. During this time of day, how much heat energy per second is lost by the cooler? And how much heat energy is lost in three hours at the water park assuming the temperature stays at 38 degrees? (Note: The thermal conductivity of Styrofoam is 0.01.)"
So you're saying their equation is incorrect, that the computation is not T2-T1, but T2-T1 + imaginary heat radiated from the cooler to the warmer