For AI: what we're learning about computations

[scruffy]

Nonlinearity-induced topological phase transition characterized by the nonlinear Chern number - Nature Physics

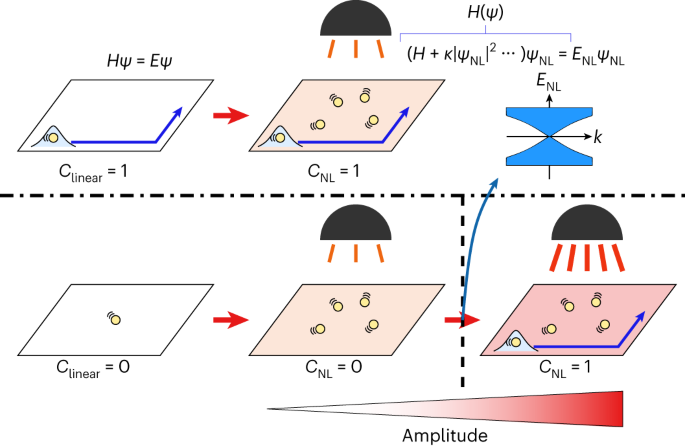
Linear topological systems can be characterized using invariants such as the Chern number. This concept can be extended to the nonlinear regime, giving rise to nonlinearity-induced topological phase transitions.

www.nature.com

The article suggests a parallel and entirely different form of computation, for AI.

Traditionally, neural networks are linear-ish, even the transformers underlying Chat-GPT.

However this linked article points to a controllable alternate form of computation based on nonlinearity and criticality.

Of immense interest are the "phase transitions" that happen in small areas of the network, which when they couple lead to a global topology.

The same thing happens in ferromagnets and also in the biological cell.

The reason it's of interest is, I want to program my own personal AI myself. Everything needed is available online, including the training datasets for natural language and the like.

 

[scruffy]

Here is a concrete example:

First this

Scientists determine gas molecules induce transition from Sierpiński triangles to one-dimensional chains

Many molecules assemble into crystalline or disordered glassy structures on surface. With certain assembly approaches, specific molecules can be made to form ordered yet aperiodic structures, such as fractals and quasicrystals. Sierpiński triangles (STs) have been prepared on surfaces and in...

phys.org

Then this

Topological synchronization of chaotic systems

Can we find order in chaos? Physicists have shown, for the first time that chaotic systems can synchronize due to stable structures that emerge from chaotic activity. These structures are known as fractals, shapes with patterns which repeat over and over again in different scales of the shape...

phys.org

 

[scruffy]

Can consciousness be explained by quantum physics? Research is closer to finding out

One of the most important open questions in science is how our consciousness is established. In the 1990s, long before winning the 2020 Nobel Prize in Physics for his prediction of black holes, physicist Roger Penrose teamed up with anaesthesiologist Stuart Hameroff to propose an ambitious answer.

sciencex.com