In the quantum world, probabilities represent "all possible paths". But what exactly is "possible"?
In physics, what's possible is determined by a model, in this case the Schrodinger equation and it's geometric embeddings.
But what if you don't know the model ahead of time?
In that case, you have to build it. The classical way of building models is Bayesian inference, which works off "hypotheses".
Linear hypotheses are asymptotic, which means the more data you get, the better you can predict. However they fail in many cases, resulting in things like Simpson's paradox. The problem is especially acute when the model involves causality - which in physics is related to irreversibility.
The general problem is we begin with unknown dimensionality. We have to look at a dataset and "estimate" how many parameters it takes to describe it. We do that by extracting correlations between data points and groups of points, and we partition the dataset in various ways while we're doing that (using fancy terms like "cluster analysis").
However there is a procedure in machine learning that successively carves out subspaces of the correlations, it's a version of "pruning" paths. In Judea Pearl's do-calculus it's called "interventions". It means removing some of the possible paths, and then rebuilding the information matrix.
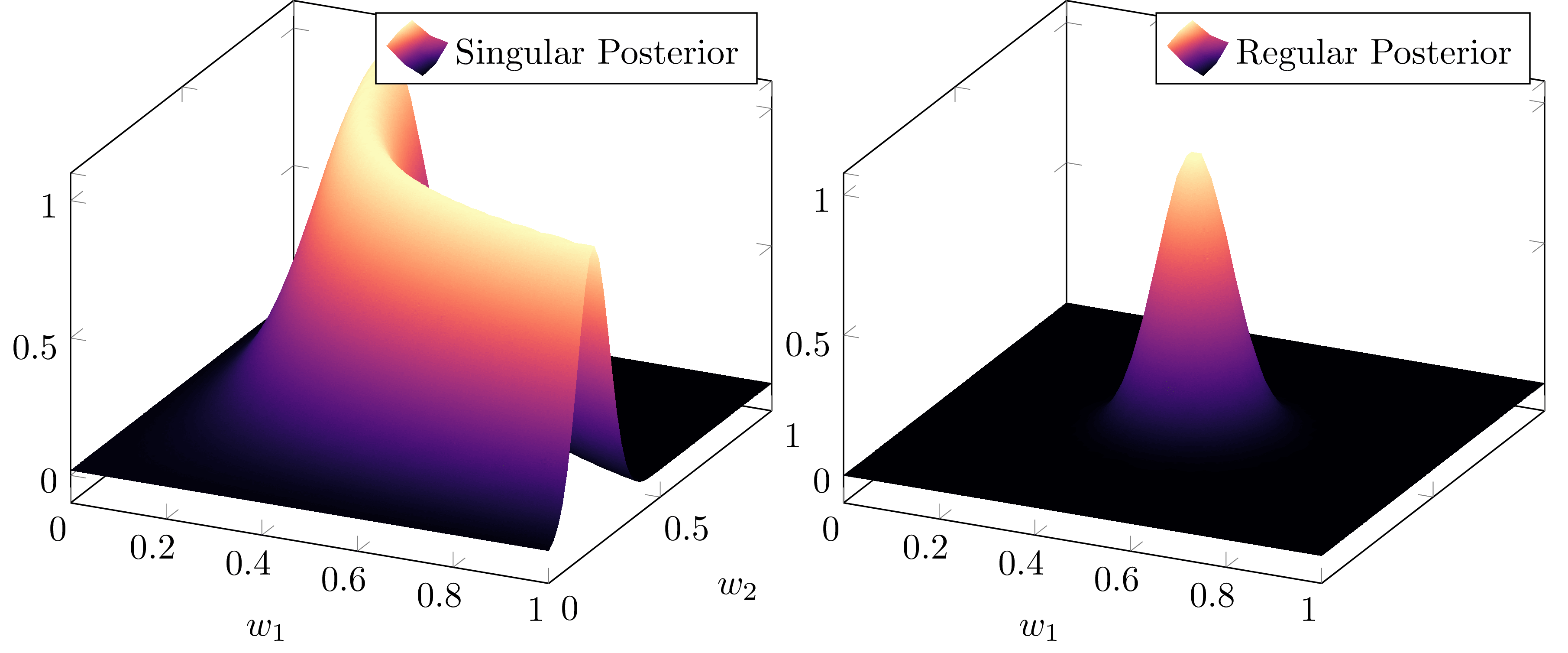
This is relevant for open systems. Which are those where the bath has an unknown composition with unknown effects. The basic idea is formulated by Sumio Watanabe, and it's more or less the same approach Renyi takes towards entropy.
 en.wikipedia.org
en.wikipedia.org
The basic idea is to identify "singular" instances of the Fisher information matrix. It turns out, neural networks are especially good at this. They can generate singular subspaces and apply them to the datasets in near real time.
Here is some background

 www.lesswrong.com
www.lesswrong.com
And further background
Here is a direct application to quantum physics
In physics, what's possible is determined by a model, in this case the Schrodinger equation and it's geometric embeddings.
But what if you don't know the model ahead of time?
In that case, you have to build it. The classical way of building models is Bayesian inference, which works off "hypotheses".
Linear hypotheses are asymptotic, which means the more data you get, the better you can predict. However they fail in many cases, resulting in things like Simpson's paradox. The problem is especially acute when the model involves causality - which in physics is related to irreversibility.
The general problem is we begin with unknown dimensionality. We have to look at a dataset and "estimate" how many parameters it takes to describe it. We do that by extracting correlations between data points and groups of points, and we partition the dataset in various ways while we're doing that (using fancy terms like "cluster analysis").
However there is a procedure in machine learning that successively carves out subspaces of the correlations, it's a version of "pruning" paths. In Judea Pearl's do-calculus it's called "interventions". It means removing some of the possible paths, and then rebuilding the information matrix.
This is relevant for open systems. Which are those where the bath has an unknown composition with unknown effects. The basic idea is formulated by Sumio Watanabe, and it's more or less the same approach Renyi takes towards entropy.
Sumio Watanabe - Wikipedia
The basic idea is to identify "singular" instances of the Fisher information matrix. It turns out, neural networks are especially good at this. They can generate singular subspaces and apply them to the datasets in near real time.
Here is some background

Singular Learning Theory - LessWrong
Singular Learning Theory (SLT) is a novel mathematical framework that expands and improves upon traditional Statistical Learning theory using techniques from algebraic geometry, bayesian statistics, and statistical physics. It has great promise for the mathematical foundations of modern machine...
And further background
Here is a direct application to quantum physics