Everyone is familiar with the concepts of "point" and "line". We generally consider that there are an infinite number of points in a line.
But here's a mindfuck.
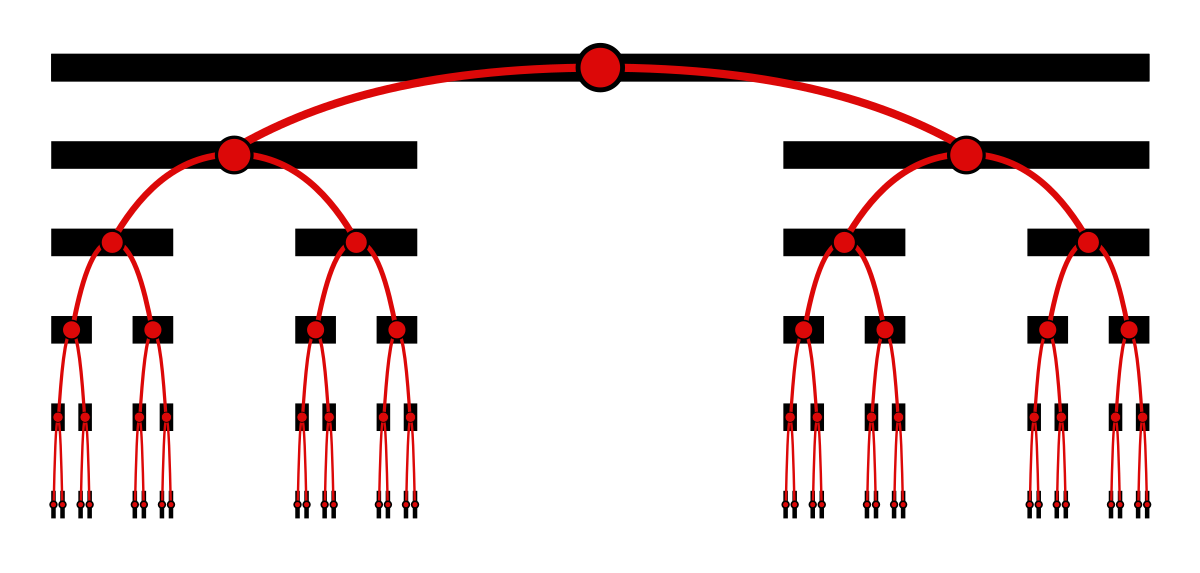
Start with a line (or a line segment). Remove the middle third. For each remaining segment, remove the middle third, and keep doing that to all remaining segments
This construction is called a Cantor Dust, and the interesting thing about it is, the dust can be proven to have THE SAME NUMBER OF POINTS AS THE LINE IT ORIGINALLY CAME FROM.
Makes no sense at all, but the math says it must be true.
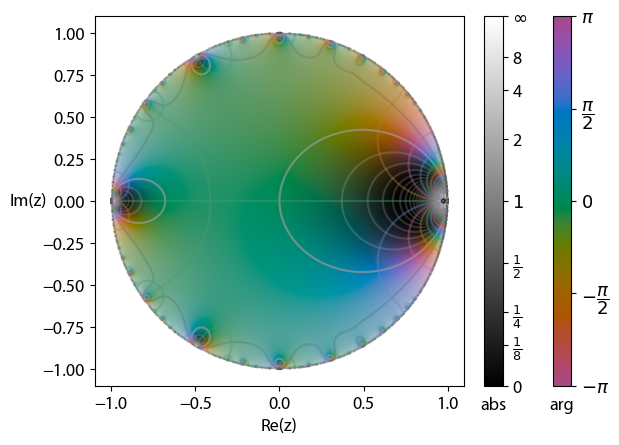
 en.wikipedia.org
en.wikipedia.org
A further surprise: the Cantor Dust is compact! Totally illogical, but the math says it must be true.
Even weirder still - the Dust can be measured and integrated. It has a Haar measure and a non-zero Hausdorff dimension, even though its Lebesgue measure is 0.
And, when the Haar measure is normalized so the set measures 1, the Cantor Dust becomes formally identical to an infinite series of coin tosses
This remarkable set is self similar (fractal) and has a conservation law associated with it, even though the set is nowhere dense.
But here's a mindfuck.
Start with a line (or a line segment). Remove the middle third. For each remaining segment, remove the middle third, and keep doing that to all remaining segments
This construction is called a Cantor Dust, and the interesting thing about it is, the dust can be proven to have THE SAME NUMBER OF POINTS AS THE LINE IT ORIGINALLY CAME FROM.
Makes no sense at all, but the math says it must be true.

Cantor set - Wikipedia
A further surprise: the Cantor Dust is compact! Totally illogical, but the math says it must be true.
Even weirder still - the Dust can be measured and integrated. It has a Haar measure and a non-zero Hausdorff dimension, even though its Lebesgue measure is 0.
And, when the Haar measure is normalized so the set measures 1, the Cantor Dust becomes formally identical to an infinite series of coin tosses
This remarkable set is self similar (fractal) and has a conservation law associated with it, even though the set is nowhere dense.